In the next two sections we’ll talk about the HashSet and HashMap data structures provided in the Java Collections Framework.
In this section we’ll cover Hash Tables, the theoretical foundation on which both of these implementations are based.
What’s a Hash Table?
Hash tables provide us with a way to efficiently map keys to values. For example, to map the name of a person (key) to their phone number (value), or to map a bank account number (key) to the bank account details that correspond to that bank account number (value).
What you use as the key and value depends on the context of the problem you’re trying to solve as shown in the 2 examples above.
For the remainder of this section, let’s assume we’re trying to map the internal identifier of an user in our system, with the details of that user, for example:
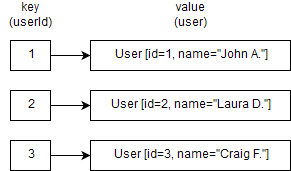
Why is it called a Hash Table?
Hash tables rely on a hash code of the key objects being stored to split/distribute values into separate buckets. In Java, the hashCode method is defined in the Object class hence we can get a hash value for all classes in our Java applications.
When using hash based data structures, it is important that the classes of the objects being stored follow the contract of the equals and hashCode methods correctly. Not doing so can lead to unexpected results or unexpected performance behaviors.
|
You can think of the buckets as an array in Java, where each bucket stores one or more objects.
Inserting elements into a Hash Table
Let’s illustrate this with our users example. First, let’s assume our hash table has 7 buckets and is empty:

Now, let’s assume we’d like to insert a User with id=100 and name="Andy G." into our hash table. Following our example, we’re using our user’s id as the key for our hash table, in this case 100.
The first step we need to take to insert this key → value mapping (100 → User [id=100, name="Andy G."]) into our hash table is to calculate the bucket it belongs to, which is a 2 step operation:
| Summary | Description | Input | Output |
|---|---|---|---|
1. Calculate the hash of the key |
In our case, the key is |
|
|
2. Calculate the index of the bucket based on the hash |
The hash value is a number that isn’t guaranteed to be in the range of the number of buckets we have. In our case we only have |
|
|
Based on this, our key→value mapping belongs to the bucket with index 2, and once inserted we could represent it like this:
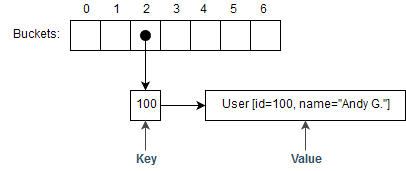
If we follow the same process for the following key → value mappings:
| Key (User Id) | Value (User object) | Index based on the hash |
|---|---|---|
|
|
|
|
|
|
We’d end with the following entries in our buckets:
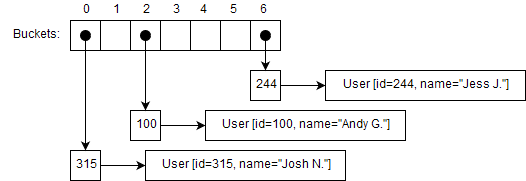
Collision handling
With the examples above, it is clear that as we add more mappings there is a higher probability that two or more keys will end up in the same bucket. When this happens, this is called a hash collision.
Hash table implementations will have different ways of resolving this problem. For the example above, we’ll assume that each bucket entry is a list of keys that can grow as much as required.
For example, if we add the mapping 9 → User [id=9, name="Paul D."], it will be added in bucket 2 and we’d end up with the following representation:
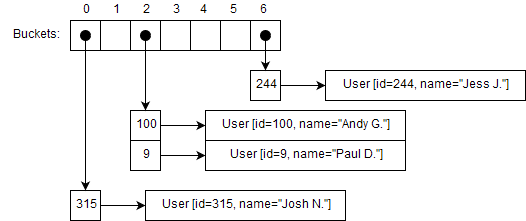
This means that bucket 2 now has 2 elements inside of it, with keys 9 and 100.
Finding a key in a hash table
One of the advantages of using a hash table is the speed of performing lookups of keys. In average, a hash table should offer constant (O(1)) look up time complexity.
This would be the equivalent of performing an indexOf(object) call in an ArrayList that has a linear (O(n)) time complexity.
| Under certain circumstances, in very small data sets with costly hash functions, it might be better to use a different data structure as the cost of calculating the hash might be higher than doing a linear search. |
Example: Find 315 in an ArrayList vs our example hash table
Let’s analyse this with an example. Let’s assume we have an ArrayList<Integer> with the 4 keys we’ve added:

If we want to find where key 315 is in our data structure:
-
For the
ArrayList<Integer>data structure, we need to do a linear search (indexOfmethod). This means, we need to go element by element and compare them with the value315. -
For the hash table case, we calculate the index of the bucket (in this case bucket
0), and compare the element in that bucket with the value we’re looking for.
In the case of the ArrayList, the search depends on the size of the list, hence it is O(n). More elements means more time to find an item.
In the case of the hash table, the search doesn’t depend on the total number of elements, hence it is O(1) in average. However, it does depend on the number of elements in a single bucket, so the one case we need to be careful about is when the number of elements per bucket starts growing too much, which leads into dynamic resizing.
Dynamic resizing
In a similar way to an ArrayList, when hash tables are considered full, they undergo a dynamic resizing process. This is done with the purpose of keeping the probability of hash collisions low to provide that O(1) average lookup time.
The resizing consists of increasing the size of our bucket array and moving all our data from the old array to the new one.
Hash tables have a load factor concept that defines when a resizing process should occur. Let’s assume that in our example our load factor is 90%:
-
Capacity=
7(the size of our bucket array) -
Load Factor=
90% -
Num of keys to resize=
7 * 90% = 6.3
This means that when we’ve added more than 6 keys to our example hash table, a resizing process will occur.
Rehashing
When a resizing process occurs, all our entries from our old bucket array need to be moved to a new bucket array that has a different size. This means that we need to perform our hashing process again for each entry to calculate the new bucket that each key should occupy.
Two notes on the hashCode method
Number one: Good hash functions are essential to this type of data structures. One common example of a valid but non-optimal hash function is one that returns the same value for all objects.
For example, if you define a class with the following hashCode method:
@Override
public int hashCode() {
return 1;
}In terms of the contract, this is a valid hashCode method. However, if you use this class as the key in a hash table you’ll end up with all keys in the same bucket, no matter how big the bucket array is.
You’ll be better using a different data structure in this case.
Number two: A common caveat of badly implemented hashCode methods is that their return value changes over time. For example, if you have an object x and at the start of your application it produces x.hashCode() ⇒ 5 and at some point down the line it produces a different hash code x.hashCode() ⇒ 7.
The common symptom is that you add object x as a key to a hash table, and then when you look for it in the hash table some time later, it can’t find it.
Remember that the bucket that will be used to look up for an item relies on the hash code. So, if you inserted the item when x had a hash code of 5, chances are that it will be stored in a different bucket than if the hash code is 7. The result is that the hash table will be looking for the item in the wrong bucket.
| Immutable classes are the best solution here. Where possible, use immutable classes for keys in your hash based data structures. |
Does this mean I should use hash tables instead of lists?
No. Remember that different data structures offer different performance characteristics and depending on your use case some options will be better than others.
For example, if you need to keep elements in order or sorted in a specific way, then a hash based data structure might not be your best option.
However, if you have a large number of elements that can be looked up by a key and you need to perform a large number of lookups, then a hash table sounds like a good candidate.