In the previous section we covered some of the basic operations we can perform with List and Collection objects, like adding objects, iterating over them, checking if an element exists, among others.
In this section we’ll cover some of the internals of the ArrayList implementation and some of it’s performance characteristics.
Another common implementation of List<E> is LinkedList<E> which we’ll not cover in this beginners course.
|
What’s an ArrayList<E>?
As mentioned in the previous section, an ArrayList<E> is a data structure that provides all the operations defined in the List contract that stores elements of type E.
Specifically, this implementation uses an array behind the scenes, but handles for us the resizing of the array when we hit its size limit.
Remember that a regular array has a defined length when it’s constructed which can’t be changed (e.g. new int[5]). The added value of an ArrayList is that it will handle the cases when we keep adding elements to the array and hit its size limit.
|
Representing an ArrayList
For the purpose of this example, let’s assume we have an ArrayList<Integer> to store integer values, like so:
// creates an ArrayList with an initial capacity enough to store 4 elements
ArrayList<Integer> numbers = new ArrayList<>(4);
numbers.add(10);
numbers.add(20);
numbers.add(30);One way to represent or think about this ArrayList visually could be the following:
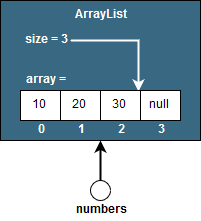
In practice though, ArrayList objects tend to be represented as a normal array for simplicity unless the internals are being described.
|
As you can see, an ArrayList keeps track of 2 things:
-
the current size of the list, and,
-
the array it is currently using to store the data; the length of this array can be greater than the size of the list and is called
capacity.
In our example, we have an ArrayList with capacity of 4 and a size of 3 as we’ve added 3 elements to our list.
Performance characteristics - Big-O notation
The way performance characteristics of operations in data structures and algorithms is denoted tends to be via the use of big-O notation. Although the details are outside of the scope of this course, it is important to understand some of the common notations.
| Notation | Name |
|---|---|
O(1) |
Constant |
O(log n) |
Logarithmic |
O(n) |
Linear |
O(nlog n) |
Log-linear |
O(n2) |
Quadratic |
| Lower is better - for example, O(1) is better than O(n) |
These values are not exact representations of the runtime of an algorithm, but serve as a point of comparison between algorithms. The n refers to the size of the input to our algorithm. In the case of data structures, n is the number of elements in the collection.
As a hypothetical example, let’s say you need to choose an algorithm to find an object in a collection with n elements. Let’s assume we find 3 algorithms:
-
One performing the search in O(1), meaning that the larger our number of elements
nin the collection, the performance of our search algorithm won’t be affected (the performance remains constant). -
A second algorithm performing the search in O(n), which means that as our number of elements
ngrows, the performance of our algorithm degrades at a linear rate with the number of elements. -
A third algorithm performing the search in O(n2), meaning that as our number of elements
ngrows, the performance of the algorithm degrades at a quadratic rate.
This type of comparison allows us to identify the best algorithm in terms of performance. In our hypothetical example we should choose the algorithm with O(1) performance.
Performance characteristics - ArrayList
As defined in the documentation for ArrayList, the following table summarizes the performance of common operations:
| Operations | Performance |
|---|---|
|
O(1) |
|
O(1) (see below) |
|
O(n) |
The add and remove operations run in O(1) if we’re adding/removing elements at/from the end of the list. If we’re adding/removing elements anywhere else, the performance becomes O(n) as all other elements in the array need to be shifted.
For example, if you add an element at the beginning of the list (index 0), all the existent elements need to be moved one position to the right before we can insert the new element.
Analysing the add(E element) method
This doesn’t intend to be a performance analysis of the add method, but instead a high level view into its behaviour under 2 different scenarios.
|
One of 2 cases can happen when we invoke add(E element) in an ArrayList:
1) If we have enough capacity, this means, if our array still has space to store a new element. In this case the element is added as the next element in our list. For example, let’s assume our numbers list above has a capacity of 4 and we invoke:
numbers.add(40);Then the following would happen:
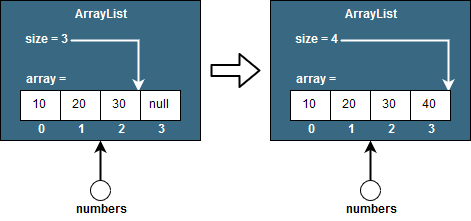
Here, the add operation didn’t depend on the size of the list, for example, we didn’t have to move/copy elements around. In this case, our operation is O(1).
2) Now, if our ArrayList has already reached its capacity limit, meaning that the length of the array and the size of the list have the same value, the ArrayList first needs to increase the capacity before being able to insert the new element.
For example, if we do:
numbers.add(50);the ArrayList will create a new internal array with more capacity than the one we currently have, copy over all the elements into the new array and then insert the element at the end as we’d do in the first case.
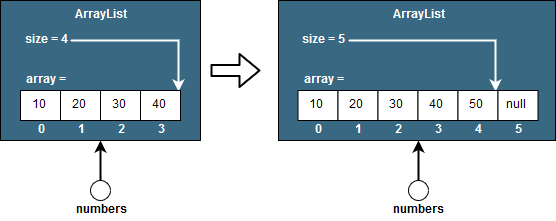
How much the internal array will grow is not specified in the API and is an implementation detail. In our example, we’re assuming the new internal array has capacity to store 6 elements in total.
Here, the add operation had to copy n elements (the size of the array) into a larger array, hence, in this particular case our operation was O(n).
When analysing this type of scenarios, most data structures will mention their amortized cost, for the case of the add method in ArrayList, it is O(1) as this second case doesn’t happen regularly.